माध्य का अर्थ :-
सांख्यिकीय माध्यों में सबसे लोकप्रिय समांतर माध्य या गणितीय माध्य है। इसी लोकप्रियता के कारण हम इसे सरल भाषा में केवल माध्य के नाम से भी पुकारते हैं। जब औसत या केंद्र बिंदु निकालने की बात आती है, तो इसका मतलब आम भाषा में माध्य निकालने से होता है। समांतर माध्य का अर्थ वह संख्या है जो किसी श्रेणी के सभी पदों के मूल्यों के योग को उनकी संख्या से भाग देकर प्राप्त की जाती है।
माध्य की परिभाषा :-
विभिन्न विद्वानों ने की परिभाषा इस प्रकार दी है-
“समांतर माध्य वह परिणाम है जो किसी चर के पदों के मूल्यों के योग को उनकी संख्या से भाग देकर प्राप्त होता है। “
घोष तथा चौधरी
“समंकमाला के पदों के मूल्यों के जोड़ में उनकी संख्या के द्वारा भाग देने से प्राप्त माध्य कहलाती है। “
सेक्रिस्ट
“किसी समंकमाला में अंकगणितीय औसत या माध्य वह अंक होता है जिसे विभिन्न पदों के मूल्यों में उनकी कुल आवृत्ति से भाग देने पर प्राप्त किया जाता है।“
एलहान्स
समांतर माध्य की विशेषताएं :-
- इसमें श्रेणी के सभी मूल्यों को समान महत्व दिया जाता है।
- आदर्श माध्य के लगभग सभी गुण समांतर माध्य में पाए जाते हैं।
- समांतर माध्य में, पदों की आवृत्ति की तुलना में पदों के मूल्यों को अधिक महत्व दिया जाता है।
- समांतर माध्य और पदों की संख्या ज्ञात होने पर पदों के मूल्यों के योग की गणना आसानी से की जा सकती है।
- केंद्रीय प्रवृत्ति को मापने का यह एक बहुत ही सरल तरीका है। यह किसी श्रेणी के सभी मूल्यों की संख्या को उसकी संख्या से विभाजित करके प्राप्त किया जाता है।
समांतर माध्य की गणना :-
समांतर माध्य की गणना दो विधियों द्वारा की जा सकती है।
- प्रत्यक्ष विधि
- लघु विधि
व्यक्तिगत मूल्यों की श्रेणी में माध्य की गणना :-
प्रत्यक्ष विधि –
श्रेणी के सभी पदों के मूल्यों को पदों की संख्या से विभाजित करने पर प्राप्त संख्या माध्य के बराबर होती है। इसे निम्न सूत्र से समझा जा सकता है।
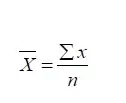
जहाँ X̄ = समांतर माध्य, ∑= योग, X =पदों का मूल्य, N =पदों की कुल संख्या,
∑ का प्रतीक ग्रीक भाषा का है। हम इसे सिग्मा कहते हैं। इसका अर्थ है योग करना।
लघु विधि –
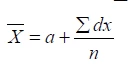
जहाँ X̄ = समांतर माध्य,, a = कल्पित माध्य, ∑= योग, dx = कल्पित माध्य से निकाला गया विचलन, n = पदों की कुल संख्या
खंडित श्रेणी में माध्य की गणना :-
प्रत्यक्ष विधि –
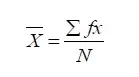
जहाँ X̄ = समांतर माध्य, ∑= योग, f = पदों की आवृत्ति, x = पदों का मूल्य, n = पदों की संख्या या आवृत्ति का योग
लघु विधि –
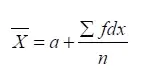
जहाँ X̄ = समांतर माध्य, a = कल्पित माध्य, ∑= योग, f = पदों की आवृत्ति, dx = कल्पित माध्य से निकाला गया विचलन dx = x – a, n = आवृत्तियों का योग
अखंडित श्रेणी या सतत श्रेणी में माध्य की गणना :-
प्रत्यक्ष विधि –
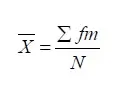
जहाँ X̄ = समांतर माध्य,. m = मध्य मूल्य = वर्गान्तर की निम्न सीमा + वर्गान्तर की उच्च सीमा/ 2, f = पदों की आवृत्ति, n = आवृत्तियों का योग
लघु विधि –
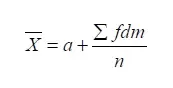
जहाँ X̄ = समांतर माध्य, a = कल्पित माध्य, ∑= योग, f = आवृत्ति, dm = कल्पित माध्य से निकाला गया विचलन, n = आवृत्तियों का योग, dm = m – a
पद विचलन विधि –
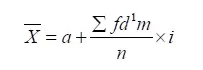
जहाँ X̄ = समांतर माध्य, a = कल्पित माध्य, ∑= योग, f =आवृत्ति, d1m = विचलनों से निकाला गया पद विचलन, d1m = dm/I = कल्पित माध्य से निकाला गया विचलन/वर्ग अन्तराल, n = आवृत्तियों का योग, i = वर्ग अन्तराल
संक्षिप्त विवरण :-
समांतर माध्य वह माध्य है जिसमें किसी समंकमाला में अंकगणितीय औसत या माध्य वह संख्या होती है जो विभिन्न पदों के मूल्यों को उनकी कुल आवृत्ति से विभाजित करने पर प्राप्त होती है। समानांतर माध्य की गणना के लिए प्रत्यक्ष विधि और लघु विधि के बारे में विवरण दिया गया है।
FAQ
माध्य क्या है?
माध्य वास्तव में एक गणितीय परिकल्पना है जो एक विशिष्ट वर्ग को विशिष्टीकरण नहीं करता है, लेकिन एक गणितीय परिणाम व्यक्त करने का एक संक्षिप्त तरीका है, जैसे कि एक चर आबादी में मानव औसत जीवन।